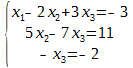В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных. Фактически, нашей целью является получение треугольной матрицы. Треугольная матрица — это матрица, у которой под главной диагональю все значения равны нулю. Пример треугольной матрицы: Рассмотрим систему линейных уравнений: Разделим обе части 1–го уравнения на a11 ≠ 0, затем: 1) умножим…
Метка: матрицы
Как решить систему линейных уравнений матричным методом?
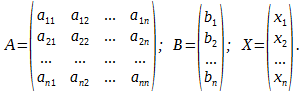
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных. Метод удобен для решения систем невысокого порядка. Матричный метод решения систем линейных уравнений Метод основан на применении свойств умножения матриц. Пусть дана система уравнений: Составим матрицы: Систему уравнений можно записать: A*X = B. Сделаем следующее преобразование: A-1*A*X = A-1*B, т.к. А-1*А = Е, то Е*Х = А-1*В Х = А-1*В Для применения данного метода необходимо находить обратную…
Как решить систему линейных уравнений методом Крамера?
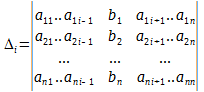
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель матрицы системы не равнялся 0. det A ≠ 0; Действительно, если какое-либо уравнение системы есть линейная комбинация остальных, то если к элементам какой-либо…
Ранг матрицы. Метод окаймляющих миноров. Линейная независимость строк (столбцов) матрицы

Пусть в матрице А размеров (m; n) выбраны произвольно k строк и k столбцов (k ≤ min(m; n)). Элементы матрицы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором Mkk порядка ky или минором k-го порядка матрицы A. Рангом матрицы называется максимальный порядок r отличных от нуля миноров матрицы A, а любой минор порядка r, отличный от нуля, — базисным минором. Обозначение: rang A = r. Если rang A = rang B и размеры матриц A и Bсовпадают, то матрицы A и B называются эквивалентными. Обозначение: A ~ B. Основными методами вычисления ранга матрицы являются метод окаймляющих миноров и…
Как найти обратную матрицу?
Для любой невырожденной матрицы А существует и притом единственная матрица A-1 такая, что A*A-1=A-1*A = E, где E — единичная матрица тех же порядков, что и А. Матрица A-1 называется обратной к матрице A. Если кто-то забыл, в единичной матрице, кроме диагонали, заполненной единицами, все остальные позиции заполнены нулями, пример единичной матрицы: Нахождение обратной матрицы методом присоединённой матрицы Обратная матрица определяется формулой: где Aij – алгебраическое дополнение элементов aij. Т.е….
Как вычислить определитель (детерминант) матрицы? Минор и алгебраическое дополнение
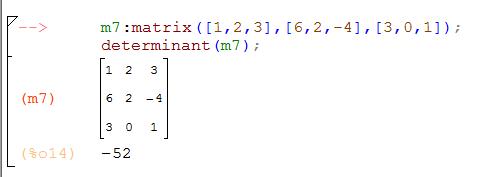
Без преобразования матрицы, определитель легко посчитать только для матриц размером 2×2 и 3×3. Это делается по формулам: Для матрицы определитель равен: a11*a22-a12*a21 Для матрицы определитель равен: a11*(a22*a33-a23*a32)-a12*(a21*a33-a23*a31)+a13*(a21*a32-a22*a31) (можно посчитать по любой строке, выше приводиться формула расчёта определителя по первой строке). Расчёты для матриц размером 4×4 и выше затруднительны, поэтому их нужно преобразовывать в соответствии со свойствами определителя. Нужно стремиться получить матрицу, в которой все значения кроме одного любого столбца или любой строки…
Произведение (перемножение) матриц

Произведением матрицы A размеров (m; k) на матрицу B размеров (k; n) называется матрица C = AB размеров (m; n) = (m; k)(k; n), каждый элемент которой получается по правилу умножения «строка на столбец»: c11 = элемент a11 первой строки матрицы A, умноженный на элемент b11 первого столбца матрицы B, элемент a12 первой строки матрицы A, умноженный на элемент b21 матрицы B, + …, + элемент a1k первой строки матрицы…