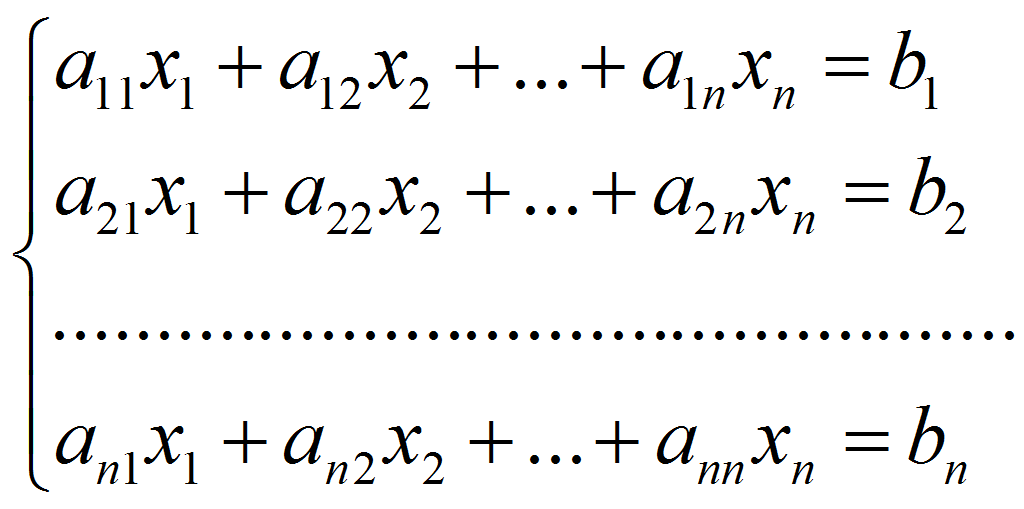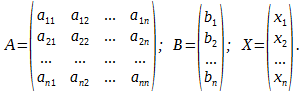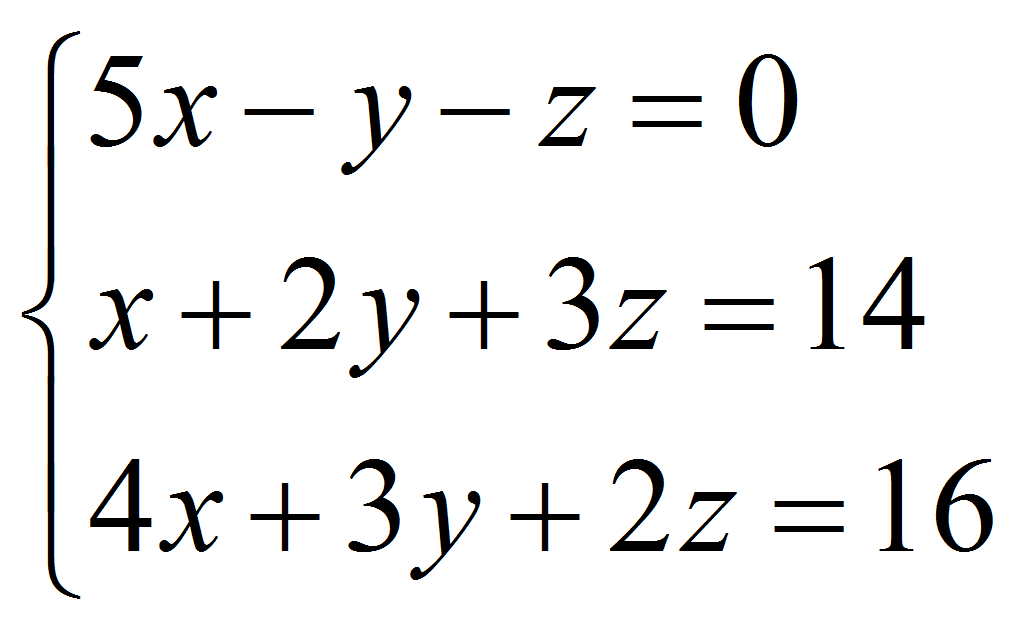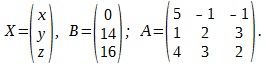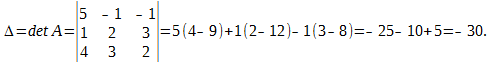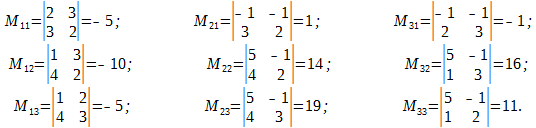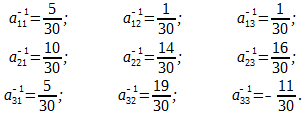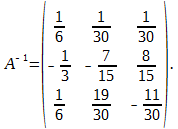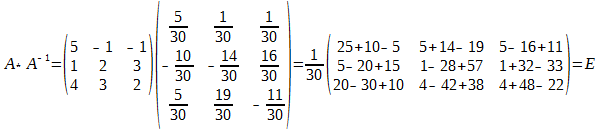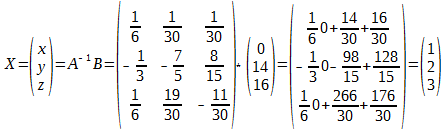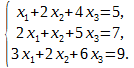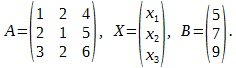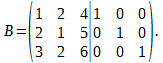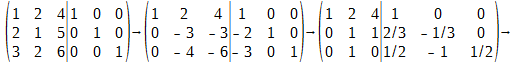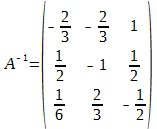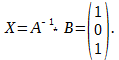Как решить систему линейных уравнений матричным методом?

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Метод удобен для решения систем невысокого порядка.

Матричный метод решения систем линейных уравнений

Метод основан на применении свойств умножения матриц.

Пусть дана система уравнений:

Составим матрицы:

Систему уравнений можно записать:

A*X = B.

Сделаем следующее преобразование: A^-1*A*X = A^-1*B,

т.к. А^-1*А = Е, то Е*Х = А^-1*В

Х = А^-1*В

Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.

Примеры решения систем линейных уравнений матричным методом

Пример. Решить систему уравнений:

Найдем обратную матрицу А^-1.

Сделаем проверку:

Находим матрицу Х.

Итого решения системы: x =1; y = 2; z = 3.

Матричным способом решить систему уравнений

Р е ш е н и е. Перепишем систему в матричном виде:  где

Решение представляется в виде X = A^-1 * B. Найдём обратную матрицу методом элементарных преобразований. Образуем матрицу B:

Обозначим строки матрицы B через α1, α2, α3. Произведём над строками матрицы B следующие преобразования:

В результате последнего получаем

Следовательно,

Имеем

матрицы система линейных уравнений Элементы линейной алгебры