Пусть в матрице А размеров (m; n) выбраны произвольно k строк и k столбцов (k ≤ min(m; n)). Элементы матрицы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором Mkk порядка ky или минором k-го порядка матрицы A. Рангом матрицы называется максимальный порядок r отличных от нуля миноров матрицы A, а любой минор порядка r, отличный от нуля, — базисным минором. Обозначение: rang A = r. Если rang A = rang B и размеры матриц A и Bсовпадают, то матрицы A и B называются эквивалентными. Обозначение: A ~ B. Основными методами вычисления ранга матрицы являются метод окаймляющих миноров и…
Месяц: Сентябрь 2016
Все подсказки дня wxMaxima
Здесь представлены те подсказки, которые мы с вами видим при запуске wxMaxima (если не отключили их показ). Некоторые показываемые подсказки на английском языке, поэтому для ликвидации этого пробела было решено их все выписать и перевести те, которые этого требуют. Здесь собраны все доступные подсказки, но убраны те, которые однозначно потеряли актуальность. Чтобы сразу приступить к использованию wxMaxima, начните вводить вашу команду. Должна появиться ячейка ввода. Затем нажмите Shift-Enter для вычисления…
Как найти обратную матрицу?
Для любой невырожденной матрицы А существует и притом единственная матрица A-1 такая, что A*A-1=A-1*A = E, где E — единичная матрица тех же порядков, что и А. Матрица A-1 называется обратной к матрице A. Если кто-то забыл, в единичной матрице, кроме диагонали, заполненной единицами, все остальные позиции заполнены нулями, пример единичной матрицы: Нахождение обратной матрицы методом присоединённой матрицы Обратная матрица определяется формулой: где Aij – алгебраическое дополнение элементов aij. Т.е….
Как вычислить определитель (детерминант) матрицы? Минор и алгебраическое дополнение
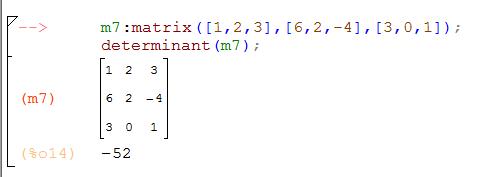
Без преобразования матрицы, определитель легко посчитать только для матриц размером 2×2 и 3×3. Это делается по формулам: Для матрицы определитель равен: a11*a22-a12*a21 Для матрицы определитель равен: a11*(a22*a33-a23*a32)-a12*(a21*a33-a23*a31)+a13*(a21*a32-a22*a31) (можно посчитать по любой строке, выше приводиться формула расчёта определителя по первой строке). Расчёты для матриц размером 4×4 и выше затруднительны, поэтому их нужно преобразовывать в соответствии со свойствами определителя. Нужно стремиться получить матрицу, в которой все значения кроме одного любого столбца или любой строки…
Произведение (перемножение) матриц

Произведением матрицы A размеров (m; k) на матрицу B размеров (k; n) называется матрица C = AB размеров (m; n) = (m; k)(k; n), каждый элемент которой получается по правилу умножения «строка на столбец»: c11 = элемент a11 первой строки матрицы A, умноженный на элемент b11 первого столбца матрицы B, элемент a12 первой строки матрицы A, умноженный на элемент b21 матрицы B, + …, + элемент a1k первой строки матрицы…

