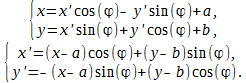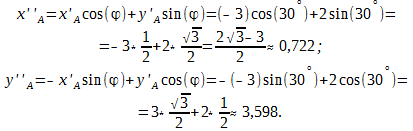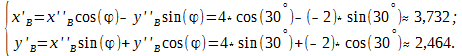Пусть новая система координат x'O'y' получается в результате параллельного переноса xOy в точку с новым началом координат O' (a; b).
Выпишем формулы для выражения старых координат x и y точки через новые x' и y'
Новые координаты точки через старые выражаются так
Пусть новая система координат x'O'y' получается поворотом старой системы xOy на угол φ. Отметим, что угол φ считается положительным, если поворот производится против часовой стрелки, и отрицательным, если по часовой.
Старые координаты точки выражаются через новые по формулам:
Новые координаты точки выражаются через старые по формулам:
При суперпозиции (т. е. при переносе и повороте осей в произвольном порядке) указанных преобразований декартовых координат связь между ними определяется формулами:
Примеры выполнения заданий с преобразованием координаты
Систему координат XOY вначале параллельно перенесли так, что новое начало стало находиться в точке O'(2,3), а затем был совершён поворот осей на угол φ = 30°. Определить новые координаты точки A, если старые координаты в системе XOY таковы: A(-1, 5). Определить, какие координаты имела точка B в старой системе XOY, если в новой системе координат она задаётся как B(4, -2).
Р е ш е н и е:
а) при параллельном переносе координат, координаты точки A станут такими:
При повороте осей на угол 30°, координаты точки A преобразуются следующим образом:
б) в системе координат XOY точка B имеет координаты:
В системе координат XOY точка B имеет координаты:
О т в е т: x''A ≈ 0,722; y''A ≈ 3,598; xB ≈ 5,732; yB ≈ 5,464.