Координаты точки и вектора

Любую совокупность действительных чисел (x₁; x₂; …;x_n) будем называть точкой, а сами числа — координатами этой точки.

Будем обозначать точки большими латинскими буквами, а координаты записывать в круглых скобках X (x₁; x₂; …;x_n).

Точку (0; 0; …;0) будем называть началом координат и обозначать O.

Пусть A(a₁; a₂; …; a_n) и B(b₁; b₂; …; b_n) – две точки. Назовём вектором величину, определяемую следующим образом: Точка A(a₁; a₂; …; a_n) называется началом вектора, а точка B(b₁; b₂; …; b_n) – концом.

Векторы также будем обозначать с помощью двух больших или одной маленькой латинских букв со стрелкой сверху, указывая их координаты в фигурных скобках:

Два вектора

с одним и тем же числом координат называются равными в том и только в том случае, если равны соответствующие координаты a₁ = b₁; a₂ = b₂; …; a_n = b_n.

Длиной (или модулем) вектора назовём величину

Вектор называется нулевым вектором.

Вектор называется противоположным вектором по отношению к вектору

и обозначается так:

Произведением вектора

на действительное число λ называется вектором

Векторы

удовлетворяющие соотношению

называются коллинеарными.

Условие коллинеарности двух векторов в векторной форме:

Условие коллинеарности двух векторов

в координатной форме таково:

Свойства операции умножения вектора на число

здесь k и λ — действительные числа.

Назовём ортами векторы, имеющие только одну координату, равную единице, при этом остальные координаты равны нулю:

Заметим, что длина орта равна единице:

Назовём двумерной декартовой прямоугольной системой координат (декартовой прямоугольной системой на плоскости) такую, которая определяется двумя ортами и , исходящими из единого начала O(0; 0), называемого началом координат. Множество концов векторов , где , коллинеарных орту , называется осью абсцисс. Множество концов векторов , где , коллинеарны орту , называется осью ординат.

Назовём трёхмерной декартовой прямоугольной системой координат (декартовой прямоугольной системой координат в пространстве) такую, которая определяется тремя ортами , и , исходящими из единого начала O(0; 0; 0), которое называется началом координат. Множество концов векторов , где , коллинеарных орту , называется осью абсцисс. Множество концов векторов , где , коллинеарных орту , называется осью ординат. Множество концов векторов , где , коллинеарных орту , называется осью аппликат.

Суммой двух векторов

с одним и тем числом координат называется вектор , координаты которого удовлетворяют условиям c_i = a_i + b_i, i = 1, 2, …, n.

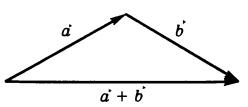
В двумерной и трёхмерной декартовых прямоугольных системах координат сложение векторов по указанному способу соответствует сложению по правилу треугольника или (что то же самое) по правилу параллелограмма.

Правило треугольника. Суммой двух векторов и называется вектор, идущий из начала вектора в конец вектора при условии, что вектор приложен к концу вектора .

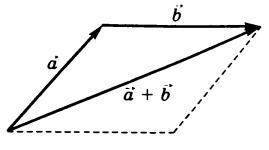
Правило параллелограмма. Если неколлинеарные векторы и приложены к общему началу и на них построен параллелограмм, то сумма + (или + ) этих векторов представляет собой диагональ указанного параллелограмма, идущую из общего начала.

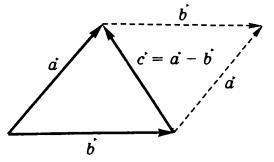
Разностью векторов

с одним и тем же числом координат называют вектор

В двумерной и трёхмерной декартовых системах координат разность векторов находится по правилу треугольника.

Свойства операции нахождения суммы векторов:

Векторы, в двумерной и трёхмерной прямоугольных декартовых системах координат могут быть соответственно представлены с помощью разложения по ортам:

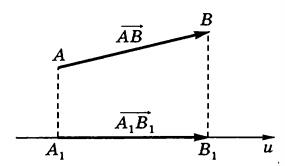
Проекцией вектора на ось u называется величина направленного отрезка оси u (A₁ и B₁ — основания перпендикуляров на ось и из точек A и B соответственно).

Координаты векторов в двумерной и трёхмерной декартовых прямоугольных системах координат равны проекциям эти векторов на соответствующие оси координат.

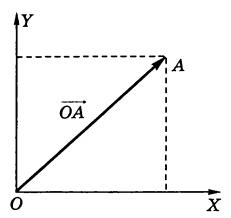
Точка A(x; y) изображается в двумерной декартовой прямоугольной системе координат как конец вектора , если начало этого вектора фиксировано в начале координат.

Примеры решения заданий по координатам точки и вектора

Даны точки A(1, 2, -2) B(3, 1, 4). Найти координаты векторов и . Найти и .

Р е ш е н и е. Координаты векторов и находятся как разности соответствующих координат конца и начала векторов, т. е. разность соответствующих координат точек A и B.

Имеем таким образом,

, т. е. .