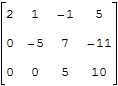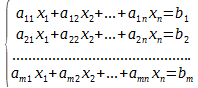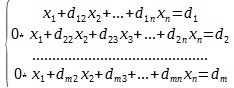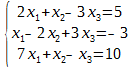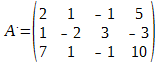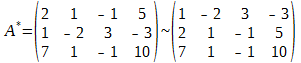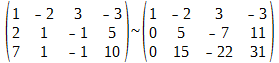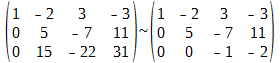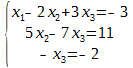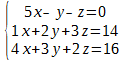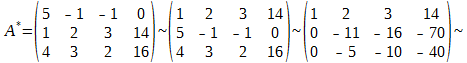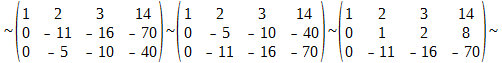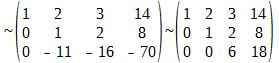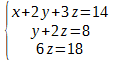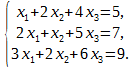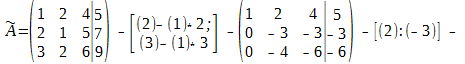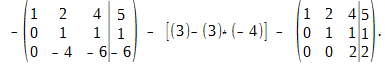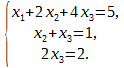Как решить систему уравнений методом Гаусса?

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Фактически, нашей целью является получение треугольной матрицы. Треугольная матрица — это матрица, у которой под главной диагональю все значения равны нулю. Пример треугольной матрицы:

Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a₁₁ ≠ 0, затем:

1) умножим на а₂₁ и вычтем из второго уравнения

2) умножим на а₃₁ и вычтем из третьего уравнения

и т.д.

Получим:

, где 

Как видим, множитель при всех x₁ во всех уравнениях, кроме первого, стал равен нулю.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

Вместо сложных формул, которые всё равно очень трудно понять, давайте перейдём сразу к примерам, они нагляднее продемонстрируют, что именно нужно делать.

Примеры решения системы уравнений методом Гаусса

Пример. Решить систему линейных уравнений методом Гаусса.

Составим расширенную матрицу системы.

Обратите внимание, что первая цифра второй строки содержит единицу. Для удобства вычисления поменяем вторую и первую строки местами (также с этой же целью можно было бы поменять местами второй и первый столбцы):

Теперь умножаем первую строку на первую цифру второй строки (т. е. на 2) и вычитаем полученную строку из этой самой второй строки. Далее умножаем первую строку на первую цифру третьей строки (т. е. на 7) и вычитаем из полученный результат из этой третьей строки:

Теперь следовало бы числа второй строки поделить на первое, отличное от нуля, число, т. е. на 5. А затем умножаем полученную строку на первое число третьей строки (отличное от нуля) и вычесть этот результат из третьей строки. Но поскольку первое ненулевое число второй строки кратно первому ненулевому числу третьей строки, то мы просто умножаем вторую строку на 3 и вычитаем из третьей строки:

Таким образом, исходная система может быть представлена в виде:

Из третьего уравнения получаем, x₃ = 2. Далее мы подставляем x₃ в третье уравнение и находим x₂ = 5. Теперь подставляем x₃ и x₂ в первое уравнение и находим x₁ = 1.

Пример. Решить систему методом Гаусса.

Составим расширенную матрицу системы, затем поменяем местами вторую и первую строки. Далее умножим первую строку на первое число второй строки (т. е. на 5) и полученную новую строку вычтем из этой самой второй строки. Также первую строку умножим на первое число третьей строки (т. е. на 4) и полученный результат вычтем из третьей строки:

Теперь поменяем вторую и третью строки местами (для упрощения расчётов), поделим все числа второй строки на одно число — на -5, это также делается для упрощения последующих расчётов.

Умножим числа второй строки на первое ненулевое число третьей строки (-11) и полученный результат вычтем из третьей строки:

Таким образом, исходная система может быть представлена в виде:

откуда получаем: z = 3; y = 2; x = 1.

Решить систему уравнений методом Гаусса

Р е ш е н и е. Имеем

На этом прямой ход метода Гаусса закончен, и для проведения обратного хода составляем систему последней матрице, эквивалентной исходной расширенной матрицы системы:

Из последнего уравнения находим x₃ = 1, подставляя найденное x₃ во второе уравнение, найдём x₂ = 1 — x₃ = 0. Из первого уравнения найдём x₁ = 5 — 2×2 — 4×3 = 1.

Заключение

Метод сводиться к получению треугольной матрицы из первоначальной расширенной матрицы. Для достижения этого результата используются элементарные преобразования матриц. При получении треугольной матрицы, из последней её строки находиться значение первой неизвестной, это значение подставляется в предпоследнее уравнение и находиться вторая неизвестная и т.д.

матрицы система линейных уравнений Элементы линейной алгебры