Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.
Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.
det A ≠ 0;
Действительно, если какое-либо уравнение системы есть линейная комбинация остальных, то если к элементам какой-либо строки прибавить элементы другой, умноженные на какое-либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Теорема. (Правило Крамера):
Система из n уравнений с n неизвестными
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
Δ = det A, а Δi – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Пример
Примеры решения систем линейных уравнений методом Крамера
Пример. Найти решение системы уравнений:
Если система однородна, т.е. bi = 0, то при Δ ≠ 0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
При Δ = 0 система имеет бесконечное множество решений.
Решить по формулам Крамера систему уравнений
Р е ш е н и е. Определитель для основной матрицы системы вычисляется так:
- Как решить систему линейных уравнений матричным методом? (100%)
- Как решить систему уравнений методом Гаусса? (100%)
- Произведение (перемножение) матриц (75.9%)
- Как вычислить определитель (детерминант) матрицы? Минор и алгебраическое дополнение (75.9%)
- Как найти обратную матрицу? (75.9%)
- Координаты точки и вектора (RANDOM - 50%)

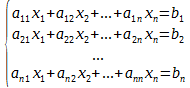
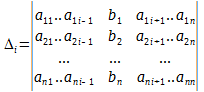
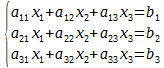
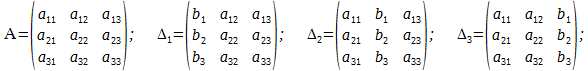

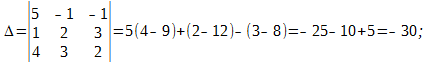
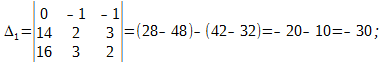

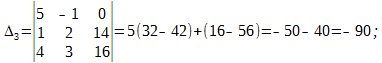
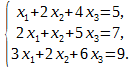
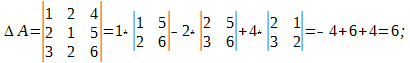
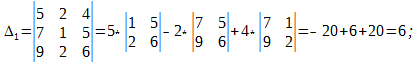
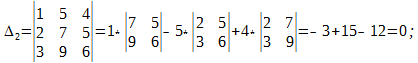
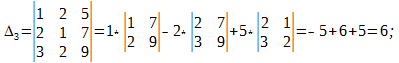
Жаль что ни слова о коде.