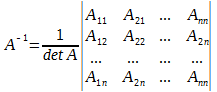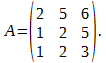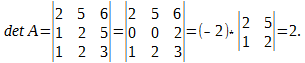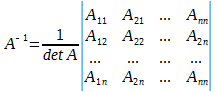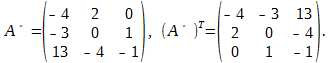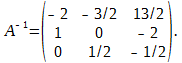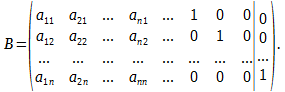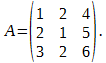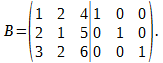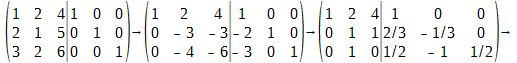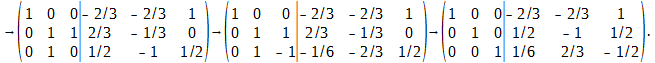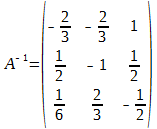Как найти обратную матрицу?

Для любой невырожденной матрицы А существует и притом единственная матрица A^-1 такая, что

A*A^-1=A^-1*A = E,

где E — единичная матрица тех же порядков, что и А. Матрица A^-1 называется обратной к матрице A.

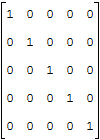
Если кто-то забыл, в единичной матрице, кроме диагонали, заполненной единицами, все остальные позиции заполнены нулями, пример единичной матрицы:

Нахождение обратной матрицы методом присоединённой матрицы

Обратная матрица определяется формулой:

где A_ij – алгебраическое дополнение элементов a_ij.

Т.е. для вычисления обратной матрицы, нужно вычислить определитель этой матрицы. Затем найти алгебраические дополнения для всех её элементов и составить из них новую матрицу. Далее нужно транспортировать эту матрицу. И каждый элемент новой матрицы поделить на определитель исходной матрицы.

Рассмотрим несколько примеров.

Найти A^-1 для матрицы

Р е ш е н и е. Найдём A^-1 методом присоединённой матрицы. Имеем det A = 2. Найдём алгебраические дополнения элементов матрицы A. В данном случае алгебраическими дополнениями элементов матрицы будут соответствующие элементы самой матрицы, взятые со знаком в соответствии с формулой

Имеем A₁₁ = 3, A₁₂ = -4, A₂₁ = -1, A₂₂ = 2. Образуем присоединённую матрицу

Транспортируем матрицу A*:

Находим обратную матрицу по формуле:

Получаем:

Методом присоединённой матрицы найти A^-1, если

Р е ш е н и е. Прежде всего вычисляем определитесь данной матрицы, чтобы убедиться в существовании обратной матрицы. Имеем

Здесь мы прибавили к элементам второй строки элементы третьей строки, умноженные предварительно на (-1), а затем раскрыли определитель по второй строке. Так как определитесь данной матрицы отличен от нуля, то обратная к ней матрица существует. Для построения присоединённой матрицы находим алгебраические дополнения элементов данной матрицы. Имеем

В соответствии с формулой

транспортируем матрицу A*:

Тогда по формуле

имеем

Нахождение обратной матрицы методом элементарных преобразований

Кроме метода нахождения обратной матрицы, вытекающего из формулы (метод присоединенной матрицы), существует метод нахождения обратной матрицы, называемый методом элементарных преобразований.

Элементарные преобразования матрицы

Элементарными преобразованиями матрицы называются следующие преобразования:

1) перестановка строк (столбцов);

2) умножение строки (столбца) на число, отличное от нуля;

3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

Для нахождения матрицы A^-1 построим прямоугольную матрицу В = (А|Е) порядков (n; 2n), приписывая к матрице А справа единичную матрицу Е через разделительную черту:

Далее, с помощью элементарных преобразований над строками, приводим матрицу В к виду (Е|А-1), что всегда возможно, если матрица А невырождена.

Рассмотрим пример.

Методом элементарных преобразований найти A^-1, если

Р е ш е н и е. Образуем матрицу B:

Обозначим строки матрицы B через α₁, α₂, α₃. Произведём над строками матрицы B следующие преобразования:

В результате последнего получаем

Следовательно, 

Нахождение обратных матриц в wxMaxima и Maxima

Для нахождения обратных матриц в wxMaxima и Maxima используется функция invert:

Эта функция равнозначна возведению матрицы в степень -1 (M^^-1).

Ещё одна функция в wxMaxima и Maxima для нахождения обратных матриц — invert_by_adjoint. Она находит обратную матрицу методом присоединения.

Также можно упомянуть функцию invert_by_lu, которая находит обратную матрицу используя LU-факторизацию.

матрицы обратная матрица элементарные преобразования матрицы Элементы линейной алгебры