1. Введение в построение графиков Maxima использует внешний пакет построения графиков для их создания (смотрите секцию форматы графиков). Функции черчения рассчитывают набор точек и передают их пакету построения графиков вместе с набором команд. Эта информация может быть передана внешней программе как по трубе или вызовом программы с указанием имени файла, где были сохранены данные. Файлу данных присваивается имя maxout_xxx.format, где xxx это уникальный номер для каждого одновременно запущенного экземпляра maxima,…
Координаты точки и вектора
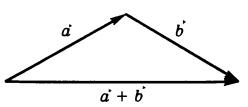
Любую совокупность действительных чисел (x1; x2; …;xn) будем называть точкой, а сами числа — координатами этой точки. Будем обозначать точки большими латинскими буквами, а координаты записывать в круглых скобках X (x1; x2; …;xn). Точку (0; 0; …;0) будем называть началом координат и обозначать O. Пусть A(a1; a2; …; an) и B(b1; b2; …; bn) – две точки. Назовём вектором величину, определяемую следующим образом: Точка A(a1; a2; …; an) называется началом…
Преобразование координат
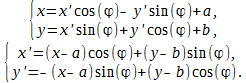
Пусть новая система координат x'O'y' получается в результате параллельного переноса xOy в точку с новым началом координат O' (a; b). Выпишем формулы для выражения старых координат x и y точки через новые x' и y' Новые координаты точки через старые выражаются так Пусть новая система координат x'O'y' получается поворотом старой системы xOy на угол φ. Отметим, что угол φ считается положительным, если поворот производится против часовой стрелки, и отрицательным, если…
Как в wxMaxima и Maxima построить графики кривых второго порядка (окружности, эллипса, гиперболы, параболы)?

Графики окружности, эллипса, гиперболы, параболы В wxMaxima и Maxima графики кривых второго порядка строятся следующим образом: load(draw); draw2d(implici(fcn,x,xmin,xmax,y,ymin,ymax)); Например: load(draw); draw2d(implicit(x^2+y^2-9,x,-4,4,y,-4,4)); Построение графиков неявных функций в wxMaxima и Maxima Примерами уравнениями неявных функций могут быть уравнения эллипса, “мнимого” эллипса, гиперболы, двух пересекающихся прямых, параболы, двух параллельных прямых, двух “мнимых” параллельных прямых, пара совпадающих прямых и окружности. Пример кривой второго порядка, заданной уравнением неявной функции (это окружность): 2×2 + 2y2 –…
Деление векторов в данном соотношении
Пусть вектор задан координатами своего начала A(ax; ay; az) и конца B(bx; by; bz) и пусть точка C(cx; cy; cz) расположена между точка A и B пусть при этом известно соотношение длин векторов тогда координаты точки C(cx; cy; cz) находятся по формулам Примеры решения заданий по делению векторов и отрезков Отрезок AB точками C(3, 4) и D(5, 6) разделён на три равные части. Найти координаты точек A и B. Р…
Как решить систему уравнений методом Гаусса?
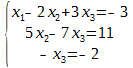
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных. Фактически, нашей целью является получение треугольной матрицы. Треугольная матрица — это матрица, у которой под главной диагональю все значения равны нулю. Пример треугольной матрицы: Рассмотрим систему линейных уравнений: Разделим обе части 1–го уравнения на a11 ≠ 0, затем: 1) умножим…
Как решить систему линейных уравнений матричным методом?
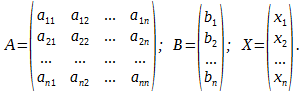
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных. Метод удобен для решения систем невысокого порядка. Матричный метод решения систем линейных уравнений Метод основан на применении свойств умножения матриц. Пусть дана система уравнений: Составим матрицы: Систему уравнений можно записать: A*X = B. Сделаем следующее преобразование: A-1*A*X = A-1*B, т.к. А-1*А = Е, то Е*Х = А-1*В Х = А-1*В Для применения данного метода необходимо находить обратную…
Как решить систему линейных уравнений методом Крамера?
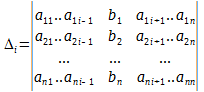
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель матрицы системы не равнялся 0. det A ≠ 0; Действительно, если какое-либо уравнение системы есть линейная комбинация остальных, то если к элементам какой-либо…
Как в wxMaxima и Maxima решить систему линейных уравнений?
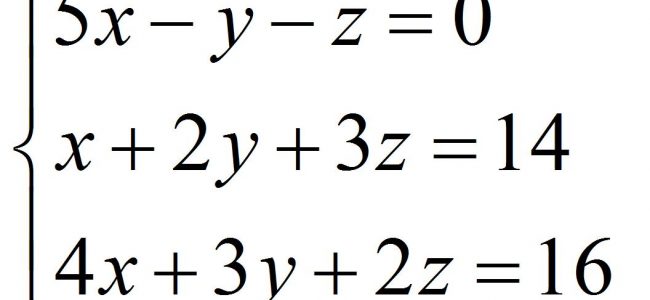
В wxMaxima / Maxima система линейных уравнений решается с помощью функции solve, которая применима и к одиночным выражениям. При вводе данных для решения системы линейных уравнений имеется особенность, не учитывая которую можно получить сообщение об ошибке. Эта особенность заключается в том, что и уравнения, и неизвестные должны представлять собой список. В wxMaxima / Maxima список – это набор данных, разделённых запятой и помещённый в квадратные скобки. Таким образом, общий вид…
Ранг матрицы. Метод окаймляющих миноров. Линейная независимость строк (столбцов) матрицы

Пусть в матрице А размеров (m; n) выбраны произвольно k строк и k столбцов (k ≤ min(m; n)). Элементы матрицы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором Mkk порядка ky или минором k-го порядка матрицы A. Рангом матрицы называется максимальный порядок r отличных от нуля миноров матрицы A, а любой минор порядка r, отличный от нуля, — базисным минором. Обозначение: rang A = r. Если rang A = rang B и размеры матриц A и Bсовпадают, то матрицы A и B называются эквивалентными. Обозначение: A ~ B. Основными методами вычисления ранга матрицы являются метод окаймляющих миноров и…
